Peta Tematik Variabel Respon
Gambar 1
Gambar 1 di atas menunjukkan peta
tematik kasus balita penderita gizi buruk di Indonesia tahun 2014. Berdasarkan
peta tersebut, provinsi di Indonesia dibagi menjadi 5 bagian. Daerah-daerah
tersebut disajikan dalam Tabel berikut:
Wilayah
|
Provinsi
|
Wilayah 1 (54 : 342)
|
Riau, Jambi, Sumsel, Bengkulu, Lampung, Kep.
Babel, Kep. Riau, DIY, Bali, Kalbar, Kalteng, Kalsel, Kaltim, Sulut, Sulsel,
Sultra, Sulbar, Maluku
|
Wilayah 2 (343 : 663)
|
Aceh, Sumbar, NTB, Sulteng, Gorontalo, Malut,
Papua Barat
|
Wilayah 3 (664 : 2242)
|
Sumut, DKI Jakarta, Banten
|
Wilayah 4 (2242 : 4107)
|
Jawa Barat, Jawa Tengah, NTT, Papua
|
Wilayah 5 (4108 : 6772)
|
Jawa Timur
|
Berdasarkan letak geografis, dapat diketahui bahwa provinsi di Indonesia memiliki jumlah kasus balita penderita gizi buruk yang cenderung berdekatan. Secara geografis, hal ini mengindikasikan bahwa terdapat pengaruh spasial pada sebaran data jumlah kasus gizi buruk. Oleh karena itu, selanjutnya akan dilakukan pengujian efek spasial secara kuantitif untuk mengetahui pengaruh spasial pada data.
Pengujian Efek Spasial
Gambar
2 tersebut
menunjukkan bahwa pola data berada pada kuadran I dan III. Hal
ini berarti bahwa provinsi dengan nilai
yang tinggi pada setiap variabel mengelompok pada
daerah yang nilainya tinggi juga dan daerah dengan nilai yang rendah
berkelompok dengan daerah yang memiliki
nilai rendah pula. Pada variabel Y, provinsi
yang memiliki angka gizi buruk yang tinggi
berkelompok dengan provinsi yang memiliki angka gizi buruk
yang tinggi pula dan provinsi yang memiliki angka
gizi buruk yang rendah berkelompok dengan angka gizi buruk
yang rendah pula. Adapun nilai masing-masing Moran’s I
pada variabel-variabel tersebut disajikan pada Tabel
berikut:
Berdasarkan
tabel diatas dan nilai I0 terlihat bahwa semua nilai Moran’s I bernilai
lebih besar dari I0 yang artinya semua variabel baik bebas maupun terikat
memiliki autokorelasi positif. Pada Gambar 2, menunjukkan bahwa
data berkelompok pada kuadran I dan III yang berarti data memiliki autokorelasi
positif.
Hasil uji
moran’s I mengindikasikan bahwa terdapat pengaruh spasial pada kasus gizi buruk
di Indonesia yakni data memiliki autokorelasi positif dan berkelompok
pada kuadran I dan III. Oleh karena asumsi spasial terpenuhi, selanjutnya
dapat dilakukan pengujian model spasial. Pada tulisan ini, akan dilakukan
pengujian model menggunakan pendekatan regresi klasik dengan metode
Ordinary Least Square (OLS) dan pendekatan spasial dengan metode Spatial
Autoregressive (SAR) dan Spatial Error Model (SEM), dari ketiga metode tersebut
selanjutnya akan dipilih model terbaik dengan cara membandingkan nilai
koefisien determinasi (R2), AIC dan SIC.
Pengujian
Model Regresi
1)
Regresi Klasik
Estimasi
parameter pada model regresi klasik dapat dilihat pada tabel berikut :
Berdasarkan tabel di atas, dengan metode regresi klasik diperoleh beberapa variabel yang signifikan pada taraf α = 5%, yakni variabel jumlah penduduk miskin (X2), persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5) dan persentase pemberian 90 tablet tambah darah pada ibu hamil (X6). Sedangkan untuk variabel persentase rumah tangga berperilaku hidup bersih (PHBS) (X1), kepadatan penduduk (X3) dan persentase pemberian vitamin A pada balita usia 6-59 bulan (X4) hasilnya tidak signifikan karena nilai p-value lebih dari alpha (α). Dengan demikian diperoleh pemodelan regresi klasik sebagai berikut:
Berdasarkan tabel di atas, dengan metode regresi klasik diperoleh beberapa variabel yang signifikan pada taraf α = 5%, yakni variabel jumlah penduduk miskin (X2), persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5) dan persentase pemberian 90 tablet tambah darah pada ibu hamil (X6). Sedangkan untuk variabel persentase rumah tangga berperilaku hidup bersih (PHBS) (X1), kepadatan penduduk (X3) dan persentase pemberian vitamin A pada balita usia 6-59 bulan (X4) hasilnya tidak signifikan karena nilai p-value lebih dari alpha (α). Dengan demikian diperoleh pemodelan regresi klasik sebagai berikut:
Ŷ = 1613,468 + 0,001 X2 + 31.860 X5 – 48.673 X6
Secara
umum, model dapat diinterpretasikan sebagai berikut:
- Jika
jumlah penduduk miskin (X2) pada suatu provinsi naik sebesar satu satuan,
dan faktor lain tetap atau konstan maka bisa menaikkan angka gizi buruk di
Indonesia sebesar 0,001.
- Jika
persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5) pada
suatu provinsi naik sebesar satu satuan, dan faktor lain tetap atau
konstan maka bisa menaikkan angka gizi buruk di Indonesia sebesar 31.860.
- Jika
persentase pemberian 90 tablet tambah darah pada ibu hamil (X6) pada suatu
provinsi naik sebesar satu satuan, dan faktor lain tetap atau konstan maka
bisa menurunkan angka gizi buruk di Indonesia sebesar 48.673.
Model
regresi yang terbentuk mempunyai nilai R2 sebesar 0,8695 atau 86,95%
yang berarti model dapat menjelaskan keragaman angka gizi buruk di Indonesia
sebesar 86,95% sedangkan sisanya sebesar 13,05% dijelaskan oleh variabel lain
diluar model. Pada pemodelan SAR diperoleh nilai AIC sebesar 521,319 dan SIC
sebesar 531,794.2) Spatial Auto Regressive (SAR)
Estimasi parameter pada model Spatial Autoregressive Model (SAR) dapat dilihat pada tabel berikut:
Variabel
|
Koefisien
|
Std. Eror
|
t-statistik
|
Probabilitas
|
W_Y
|
-0,0734
|
0,0925
|
-0,7930
|
0,4277
|
Konstanta
|
1739,913
|
650,6477
|
2,6741
|
0,0074
|
X1
|
9,0532
|
7,5820
|
1,1940
|
0,2324
|
X2
|
0,0012
|
0,0001
|
11,5684
|
0,0000
|
X3
|
0,1012
|
0,0496
|
2,0397
|
0,0413
|
X4
|
2,1204
|
15,6115
|
0,1358
|
0,8919
|
X5
|
31,7524
|
7,4691
|
4,2511
|
0,0000
|
X6
|
-53,0555
|
17,0017
|
-3,1205
|
0,0018
|
R-Square = 0,8713
AIC = 522,908
SIC = 534,88
| ||||
Dari output di atas dapat dilihat bahwa dengan metode SAR menghasilkan variabel
signifikan pada taraf α = 5% yang berbeda dengan metode OLS yaitu diantaranya
variabel jumlah penduduk miskin (X2), kepadatan penduduk (X3), persentase bayi
usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5) dan persentase pemberian 90
tablet tambah darah pada ibu hamil (X6). Sedangkan persentase rumah tangga
berperilaku hidup bersih (PHBS) (X1) dan persentase pemberian vitamin A pada
balita usia 6-59 bulan (X4) hasilnya tidak signifikan karena nilai p-value
lebih dari alpha (α). Secara umum model SAR yang menggunakan taraf signifikan
5% dapat dinyatakan sebagai berikut:
Ŷ= 1739,913 – 0,0734 Wy+ 0,0012X2 + 0,1012X3 + 31,7524X5 –
53,0555X6
Keterangan
:
Y
= Jumlah kasus balita penderita gizi buruk di Indonesia
X1
= Persentase rumah tangga berperilaku hidup bersih (PHBS)
X3
= kepadatan penduduk
X5
= Persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif
X6
= persentase pemberian 90 tablet tambah darah pada ibu hamil
Secara
umum, model dapat diinterpretasikan sebagai berikut:
- Jika
jumlah penduduk miskin (X2), pada suatu provinsi naik sebesar satu satuan,
dan faktor lain tetap atau konstan maka bisa menaikkan angka gizi buruk di
Indonesia sebesar 0,0012.
- Jika
kepadatan penduduk (X3) pada suatu provinsi naik sebesar satu satuan, dan
faktor lain tetap atau konstan maka bisa menaikkan angka gizi buruk di
Indonesia sebesar 0,1012.
- Jika
persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5) pada
suatu provinsi naik sebesar satu satuan, dan faktor lain tetap atau
konstan maka bisa menaikkan angka gizi buruk di Indonesia sebesar 31,7524.
- Jika
persentase pemberian 90 tablet tambah darah pada ibu hamil (X6) pada suatu
provinsi naik sebesar satu satuan, dan faktor lain tetap atau konstan maka
bisa menurunkan angka gizi buruk di Indonesia sebesar 53,0555.
Model
regresi yang terbentuk mempunyai nilai R2 sebesar
0,87139 atau 87,139% yang berarti model dapat menjelaskan keragaman angka gizi
buruk di Indonesia sebesar 87,139% sedangkan sisanya sebesar 12,861% dijelaskan
oleh variabel lain diluar model. Pada pemodelan SAR diperoleh nilai AIC sebesar
522,908 dan SIC sebesar 534,88.3) Spatial Error Model (SEM)
Estimasi
parameter pada model Spatial Error Model (SEM) dapat dilihat pada tabel
berikut:
Variabel
|
Koefisien
|
Std. Eror
|
t-statistik
|
Probabilitas
|
Konstanta
|
1673,508
|
485,1695
|
3,4493
|
0,0005
|
X1
|
12,8901
|
7,3433
|
1,7553
|
0,0792
|
X2
|
0,0011
|
6,5806
|
17,0902
|
0,0000
|
X3
|
0,0974
|
0,0041
|
2,3439
|
0,0190
|
X4
|
9,6314
|
14,9434
|
0,6445
|
0,5192
|
X5
|
26,1333
|
7,2007
|
3,6292
|
0,0002
|
X6
|
-58,7818
|
16,2959
|
-3,6071
|
0,0003
|
LAMBDA
|
-0,3490
|
0,1903
|
-1,8338
|
0,0666
|
R-Square = 0,8819
AIC = 519,421
SIC = 529,897
| ||||
Dengan metode SEM seperti pada gambar diatas, didapatkan model regresi SEM
seperti berikut ini:
Y=1673,508+0,001X2+0,0974X3+26,1333X5-58,7818X3+u
dengan
u=-0,3490Wu+ε
Pada
model regresi SEM, pengaruh korelasi spasial diakomodir dalam model dengan memasukkan
variabel penimbang spasial LAMBDA. Hasil analisis SEM diperoleh empat variabel
yang signifikan, yaitu jumlah penduduk miskin (X2), kepadatan penduduk (X3),
persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5), dan
persentase pemberian 90 tablet tambah darah pada ibu hamil (X6). Nilai
R-Squared sebesar 0,8819 atau 88,19% menunjukkan bahwa kemampuan model
menjelaskan kasus gizi buruk di Indonesia sebesar 88,19% sedangkan sisanya
sebesar 11,81% dijelaskan oleh variabel lain diluar model. Pada pemodelan SEM
diperoleh nilai AIC sebesar 519,421 dan SIC sebesar 529,897.
Secara
umum, model dapat diinterpretasikan sebagai berikut :
- Jika
jumlah penduduk miskin (X2) di suatu provinsi naik sebesar satu satuan dan
faktor lain dianggap konstan, maka bisa menambah gizi buruk sebesar 0,001.
- Jika
kepadatan penduduk (X3) pada suatu provinsi naik sebesar satu satuan, dan
faktor lain tetap atau konstan maka bisa menaikkan angka gizi buruk di
Indonesia sebesar 0,0974.
- Jika
persentase bayi usia 0-6 bulan yang mendapatkan ASI Ekslusif (X5) pada
suatu provinsi naik sebesar satu satuan, dan faktor lain tetap atau
konstan maka bisa menaikkan angka gizi buruk di Indonesia sebesar 26,1333.
- Jika
persentase pemberian 90 tablet tambah darah pada ibu hamil (X6) pada suatu
provinsi naik sebesar satu satuan, dan faktor lain tetap atau konstan maka
bisa menurunkan angka gizi buruk di Indonesia sebesar 58,7818.
Pemilihan
Model Terbaik
Pemilihan
model terbaik antara model regresi klasik, SAR dan SEM bertujuan untuk mengetahui
model mana yang lebih baik diterapkan pada kasus balita penderita gizi buruk di
Indonesia. Kriteria kebaikan model yang digunakan adalah dengan membandingkan
nilai R2, nilai AIC (Akaike’s Information Criterion) dan nilai SIC (Schwarz
Information Criterion) dari ketiga model tersebut. Berikut perbandingan
modelnya.
Model
|
R2
|
AIC
|
SIC
|
Regresi
Klasik
|
86,95%
|
521,319
|
531,794
|
SAR
|
87,13%
|
522,908
|
534,88
|
SEM
|
88,19%
|
519,421
|
529,897
|
Berdasarkan Tabel di atas terlihat bahwa model dengan nilai R2 terbesar adalah dengan
model SEM, nilai AIC terkecil yaitu model SEM dan nilai SIC terkecil yaitu
model SEM. Sehingga model SEM lebih baik digunakan untuk menganalisis data
kasus balita penderita gizi buruk dibandingkan dengan model regresi klasik dan
SAR.
Demikian
Semoga Bermanfaat










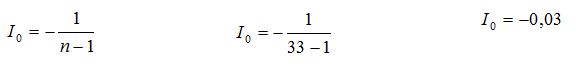






![[Pembahasan] Analisis Regresi dengan Variabel Dummy dengan SPSS [Pembahasan] Analisis Regresi dengan Variabel Dummy dengan SPSS](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUznT5C5FkWyLv3z4su2wvms3lPC07J9NvyzvYSxw6bL_1ZN7AeKVEx6LjsEU_Y9xzTztAtdqIw9ZBDptr4z17aiRsPfarkS1jdVqSYDfD91EHoEiJFYP4NHAEcJqMFjQJD4lepk4QfVdj/s72-c/Untitled-1.jpg)



3 comments
Write commentskak mau tanya, kakak kan pake aplikasi open Geoda untuk melihat hasil output SAR, SEM dan OLS. Nah mau tanya untuk aplikasi Geoda sendiri selalu menggunakan alfa 5% atau gimana ya kak itu? masih bingung dipemilihan alfanya
ReplyKalau untuk defaultnya memang 0.5, untuk alfa yang selain itu saya belum pernah coba mb, itu dulu saya pakai geoda cuma buat keperluan analisis spasial, tidak secara spesifik mempelajari aplikasi itu, mungkin lebih jelasnya mbaknya bisa belajar lewat buku tutorial geoda, bisa buka di link:
Replywww.csiss.org/clearinghouse/GeoDa/geodaworkbook.pdf
Manatau ada jawabannya disana mbak, terimakasih
Semoga bermanfaat :)
interpretasi koefisien Wy dan Wu gmn mas?
Reply:) :( hihi :-) :D =D :-d ;( ;-( @-) :P :o -_- (o) :p :-? (p) :-s (m) 8-) :-t :-b b-( :-# =p~ $-) (y) (f) x-) (k) (h) cheer lol rock angry @@ :ng pin poop :* :v 100